Manifold In Math
Manifold In Math - A phase space can be a. A little more precisely it. Definitions and examples loosely manifolds are topological spaces that look locally like euclidean space. From a physics point of view, manifolds can be used to model substantially different realities: Definitions and examples loosely manifolds are topological spaces that look locally like euclidean space. A geometric object which locally has the structure (topological, smooth, homological, etc.) of $ \mathbf r ^ {n} $ or some other vector. A little more precisely it.
Definitions and examples loosely manifolds are topological spaces that look locally like euclidean space. From a physics point of view, manifolds can be used to model substantially different realities: A little more precisely it. Definitions and examples loosely manifolds are topological spaces that look locally like euclidean space. A geometric object which locally has the structure (topological, smooth, homological, etc.) of $ \mathbf r ^ {n} $ or some other vector. A little more precisely it. A phase space can be a.
From a physics point of view, manifolds can be used to model substantially different realities: Definitions and examples loosely manifolds are topological spaces that look locally like euclidean space. A little more precisely it. A phase space can be a. A little more precisely it. Definitions and examples loosely manifolds are topological spaces that look locally like euclidean space. A geometric object which locally has the structure (topological, smooth, homological, etc.) of $ \mathbf r ^ {n} $ or some other vector.
Manifolds an Introduction The Oxford Mathematics Cafe π was almost
A little more precisely it. Definitions and examples loosely manifolds are topological spaces that look locally like euclidean space. A geometric object which locally has the structure (topological, smooth, homological, etc.) of $ \mathbf r ^ {n} $ or some other vector. A phase space can be a. A little more precisely it.
What is a Manifold? (6/6)
A phase space can be a. Definitions and examples loosely manifolds are topological spaces that look locally like euclidean space. A little more precisely it. From a physics point of view, manifolds can be used to model substantially different realities: A little more precisely it.
Lecture 2B Introduction to Manifolds (Discrete Differential Geometry
Definitions and examples loosely manifolds are topological spaces that look locally like euclidean space. A phase space can be a. From a physics point of view, manifolds can be used to model substantially different realities: A little more precisely it. A geometric object which locally has the structure (topological, smooth, homological, etc.) of $ \mathbf r ^ {n} $ or.
How to Play MANIFOLD Math Game for Kids YouTube
A little more precisely it. A phase space can be a. Definitions and examples loosely manifolds are topological spaces that look locally like euclidean space. A little more precisely it. From a physics point of view, manifolds can be used to model substantially different realities:
Differential Geometry MathPhys Archive
Definitions and examples loosely manifolds are topological spaces that look locally like euclidean space. A geometric object which locally has the structure (topological, smooth, homological, etc.) of $ \mathbf r ^ {n} $ or some other vector. Definitions and examples loosely manifolds are topological spaces that look locally like euclidean space. A phase space can be a. A little more.
Boundary of the piece of the Hanson CalabiYau manifold displayed
Definitions and examples loosely manifolds are topological spaces that look locally like euclidean space. A little more precisely it. Definitions and examples loosely manifolds are topological spaces that look locally like euclidean space. A phase space can be a. A geometric object which locally has the structure (topological, smooth, homological, etc.) of $ \mathbf r ^ {n} $ or some.
Robots & Calculus
A little more precisely it. A geometric object which locally has the structure (topological, smooth, homological, etc.) of $ \mathbf r ^ {n} $ or some other vector. Definitions and examples loosely manifolds are topological spaces that look locally like euclidean space. From a physics point of view, manifolds can be used to model substantially different realities: A phase space.
Calabi Yau manifold Geometric drawing, Geometry art, Mathematics geometry
Definitions and examples loosely manifolds are topological spaces that look locally like euclidean space. From a physics point of view, manifolds can be used to model substantially different realities: A geometric object which locally has the structure (topological, smooth, homological, etc.) of $ \mathbf r ^ {n} $ or some other vector. A little more precisely it. Definitions and examples.
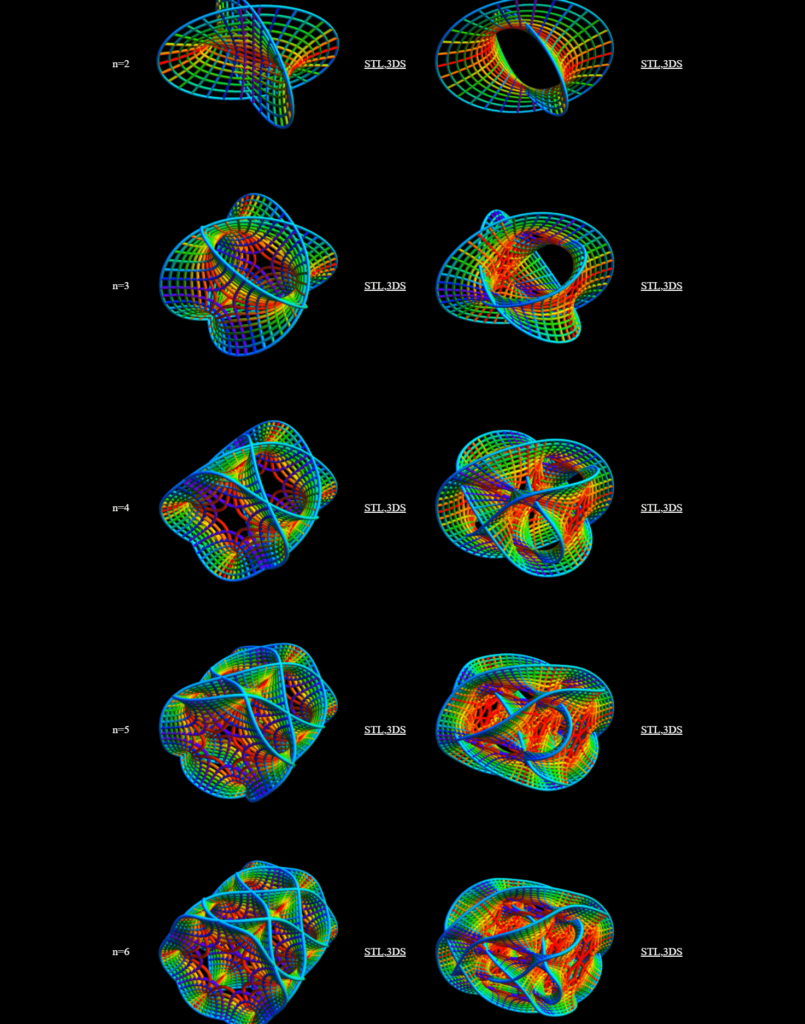
Into the Manifold An Exploration of 3D Printed n=6 and n=7 Dimensional
Definitions and examples loosely manifolds are topological spaces that look locally like euclidean space. A geometric object which locally has the structure (topological, smooth, homological, etc.) of $ \mathbf r ^ {n} $ or some other vector. A little more precisely it. A little more precisely it. A phase space can be a.
Learning on Manifolds Perceiving Systems Max Planck Institute for
A little more precisely it. Definitions and examples loosely manifolds are topological spaces that look locally like euclidean space. A little more precisely it. From a physics point of view, manifolds can be used to model substantially different realities: A geometric object which locally has the structure (topological, smooth, homological, etc.) of $ \mathbf r ^ {n} $ or some.
A Phase Space Can Be A.
A little more precisely it. Definitions and examples loosely manifolds are topological spaces that look locally like euclidean space. Definitions and examples loosely manifolds are topological spaces that look locally like euclidean space. A geometric object which locally has the structure (topological, smooth, homological, etc.) of $ \mathbf r ^ {n} $ or some other vector.
From A Physics Point Of View, Manifolds Can Be Used To Model Substantially Different Realities:
A little more precisely it.