Parametric Form Of An Ellipse
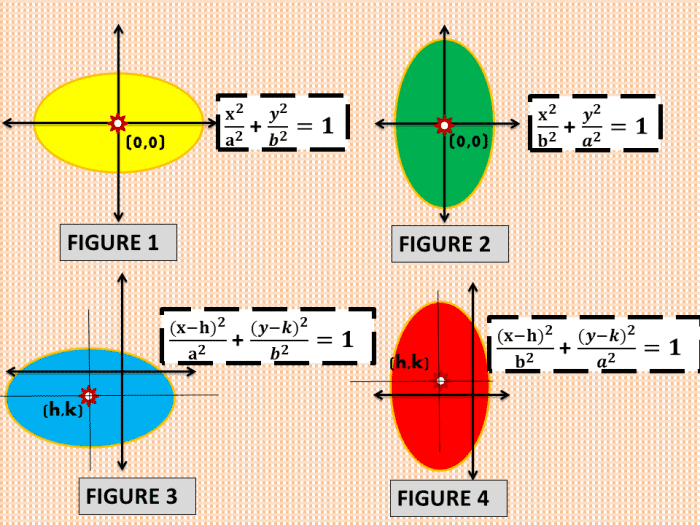
Parametric Form Of An Ellipse - Consider the ellipse given by \(\frac{x^2}{9} + \frac{y^2}{4} = 1.\) what are the parametric equations for this ellipse? I know that $a=2$ and $b=1$ (where $a$ and $b$ are the axis of the ellipse), so i parameterize as: The general form of this ellipse is $$a x^2 + b x y + c y^2 = 1$$ the idea is to find the coefficients; This is done by expanding the sines and forming.
Consider the ellipse given by \(\frac{x^2}{9} + \frac{y^2}{4} = 1.\) what are the parametric equations for this ellipse? This is done by expanding the sines and forming. I know that $a=2$ and $b=1$ (where $a$ and $b$ are the axis of the ellipse), so i parameterize as: The general form of this ellipse is $$a x^2 + b x y + c y^2 = 1$$ the idea is to find the coefficients;
The general form of this ellipse is $$a x^2 + b x y + c y^2 = 1$$ the idea is to find the coefficients; I know that $a=2$ and $b=1$ (where $a$ and $b$ are the axis of the ellipse), so i parameterize as: Consider the ellipse given by \(\frac{x^2}{9} + \frac{y^2}{4} = 1.\) what are the parametric equations for this ellipse? This is done by expanding the sines and forming.
Normal of an Ellipse L9 Three Equations 1 Parametric form 2 Point
This is done by expanding the sines and forming. The general form of this ellipse is $$a x^2 + b x y + c y^2 = 1$$ the idea is to find the coefficients; Consider the ellipse given by \(\frac{x^2}{9} + \frac{y^2}{4} = 1.\) what are the parametric equations for this ellipse? I know that $a=2$ and $b=1$ (where $a$.
Wie man eine Ellipse mit einer gegebenen Gleichung grafisch darstellt
The general form of this ellipse is $$a x^2 + b x y + c y^2 = 1$$ the idea is to find the coefficients; Consider the ellipse given by \(\frac{x^2}{9} + \frac{y^2}{4} = 1.\) what are the parametric equations for this ellipse? This is done by expanding the sines and forming. I know that $a=2$ and $b=1$ (where $a$.
Parametric Equations Conic Sections
Consider the ellipse given by \(\frac{x^2}{9} + \frac{y^2}{4} = 1.\) what are the parametric equations for this ellipse? This is done by expanding the sines and forming. I know that $a=2$ and $b=1$ (where $a$ and $b$ are the axis of the ellipse), so i parameterize as: The general form of this ellipse is $$a x^2 + b x y.
S 2.26 Parametric Equation of Ellipse How to Find Parametric Equation
I know that $a=2$ and $b=1$ (where $a$ and $b$ are the axis of the ellipse), so i parameterize as: This is done by expanding the sines and forming. The general form of this ellipse is $$a x^2 + b x y + c y^2 = 1$$ the idea is to find the coefficients; Consider the ellipse given by \(\frac{x^2}{9}.
Equation of Ellipse in parametric form
This is done by expanding the sines and forming. Consider the ellipse given by \(\frac{x^2}{9} + \frac{y^2}{4} = 1.\) what are the parametric equations for this ellipse? The general form of this ellipse is $$a x^2 + b x y + c y^2 = 1$$ the idea is to find the coefficients; I know that $a=2$ and $b=1$ (where $a$.
How to Graph an Ellipse Given an Equation Owlcation
Consider the ellipse given by \(\frac{x^2}{9} + \frac{y^2}{4} = 1.\) what are the parametric equations for this ellipse? I know that $a=2$ and $b=1$ (where $a$ and $b$ are the axis of the ellipse), so i parameterize as: This is done by expanding the sines and forming. The general form of this ellipse is $$a x^2 + b x y.
Ex Find Parametric Equations For Ellipse Using Sine And Cosine From a
The general form of this ellipse is $$a x^2 + b x y + c y^2 = 1$$ the idea is to find the coefficients; I know that $a=2$ and $b=1$ (where $a$ and $b$ are the axis of the ellipse), so i parameterize as: This is done by expanding the sines and forming. Consider the ellipse given by \(\frac{x^2}{9}.
How to Write the Parametric Equations of an Ellipse in Rectangular Form
This is done by expanding the sines and forming. The general form of this ellipse is $$a x^2 + b x y + c y^2 = 1$$ the idea is to find the coefficients; Consider the ellipse given by \(\frac{x^2}{9} + \frac{y^2}{4} = 1.\) what are the parametric equations for this ellipse? I know that $a=2$ and $b=1$ (where $a$.
Ellipse Equation, Properties, Examples Ellipse Formula
I know that $a=2$ and $b=1$ (where $a$ and $b$ are the axis of the ellipse), so i parameterize as: This is done by expanding the sines and forming. The general form of this ellipse is $$a x^2 + b x y + c y^2 = 1$$ the idea is to find the coefficients; Consider the ellipse given by \(\frac{x^2}{9}.
tangent at vertex of ellipse, parametric form, focal length, auxiliary ci..
The general form of this ellipse is $$a x^2 + b x y + c y^2 = 1$$ the idea is to find the coefficients; Consider the ellipse given by \(\frac{x^2}{9} + \frac{y^2}{4} = 1.\) what are the parametric equations for this ellipse? I know that $a=2$ and $b=1$ (where $a$ and $b$ are the axis of the ellipse), so.
The General Form Of This Ellipse Is $$A X^2 + B X Y + C Y^2 = 1$$ The Idea Is To Find The Coefficients;
This is done by expanding the sines and forming. I know that $a=2$ and $b=1$ (where $a$ and $b$ are the axis of the ellipse), so i parameterize as: Consider the ellipse given by \(\frac{x^2}{9} + \frac{y^2}{4} = 1.\) what are the parametric equations for this ellipse?