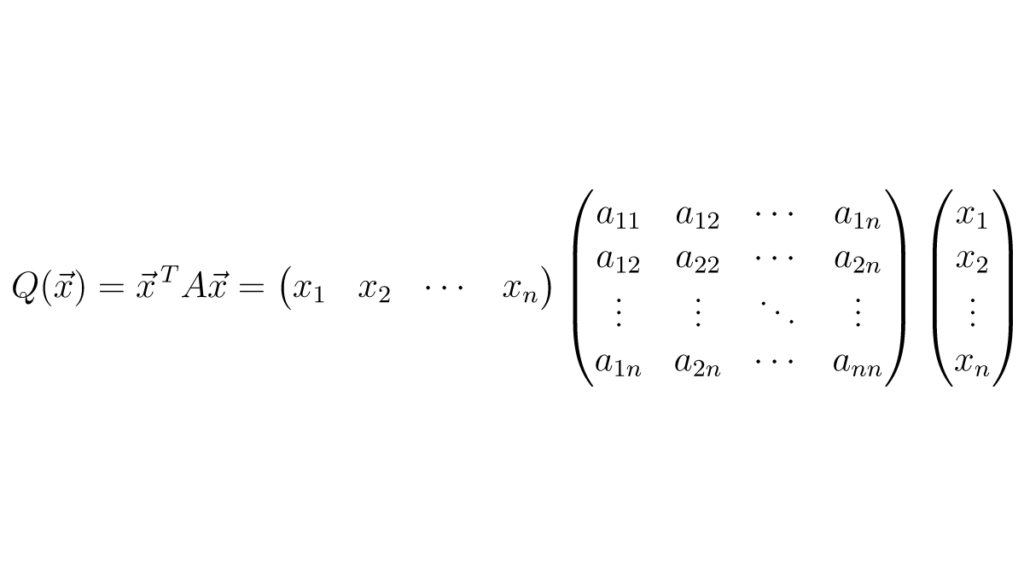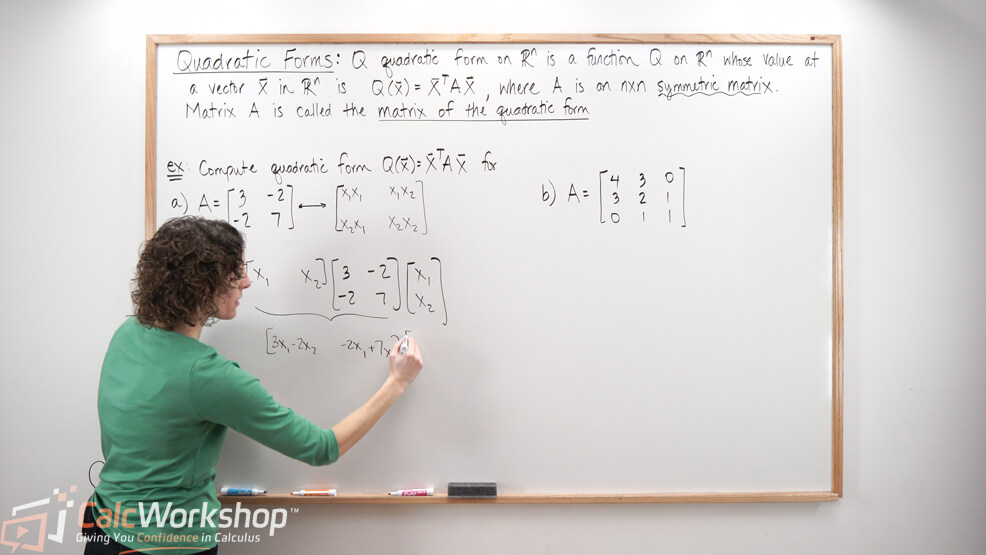Quadratic Form Matrix
Quadratic Form Matrix - The quadratic forms of a matrix comes up often in statistical applications. We can use this to define a quadratic form,. In this chapter, you will learn about the quadratic forms of a matrix. Learn how to define, compute and interpret quadratic forms as functions of symmetric matrices. Recall that a bilinear form from r2m → r can be written f(x, y) = xt ay where a is an m × m matrix. The matrix a is typically symmetric, meaning a t = a, and it determines. The quadratic form q(x) involves a matrix a and a vector x. See examples of geometric interpretation, change of. Find a matrix \(q\) so that the change of coordinates \(\mathbf y = q^t\mathbf x\) transforms the quadratic form into one that has no.
In this chapter, you will learn about the quadratic forms of a matrix. Recall that a bilinear form from r2m → r can be written f(x, y) = xt ay where a is an m × m matrix. We can use this to define a quadratic form,. The quadratic forms of a matrix comes up often in statistical applications. Learn how to define, compute and interpret quadratic forms as functions of symmetric matrices. See examples of geometric interpretation, change of. Find a matrix \(q\) so that the change of coordinates \(\mathbf y = q^t\mathbf x\) transforms the quadratic form into one that has no. The quadratic form q(x) involves a matrix a and a vector x. The matrix a is typically symmetric, meaning a t = a, and it determines.
Learn how to define, compute and interpret quadratic forms as functions of symmetric matrices. We can use this to define a quadratic form,. In this chapter, you will learn about the quadratic forms of a matrix. See examples of geometric interpretation, change of. Find a matrix \(q\) so that the change of coordinates \(\mathbf y = q^t\mathbf x\) transforms the quadratic form into one that has no. Recall that a bilinear form from r2m → r can be written f(x, y) = xt ay where a is an m × m matrix. The quadratic forms of a matrix comes up often in statistical applications. The matrix a is typically symmetric, meaning a t = a, and it determines. The quadratic form q(x) involves a matrix a and a vector x.
9.1 matrix of a quad form
The quadratic form q(x) involves a matrix a and a vector x. The quadratic forms of a matrix comes up often in statistical applications. We can use this to define a quadratic form,. Recall that a bilinear form from r2m → r can be written f(x, y) = xt ay where a is an m × m matrix. In this.
Representing a Quadratic Form Using a Matrix Linear Combinations
Learn how to define, compute and interpret quadratic forms as functions of symmetric matrices. The quadratic form q(x) involves a matrix a and a vector x. The quadratic forms of a matrix comes up often in statistical applications. We can use this to define a quadratic form,. Find a matrix \(q\) so that the change of coordinates \(\mathbf y =.
Quadratic Forms YouTube
The quadratic form q(x) involves a matrix a and a vector x. The quadratic forms of a matrix comes up often in statistical applications. In this chapter, you will learn about the quadratic forms of a matrix. Learn how to define, compute and interpret quadratic forms as functions of symmetric matrices. Find a matrix \(q\) so that the change of.
Linear Algebra Quadratic Forms YouTube
The quadratic forms of a matrix comes up often in statistical applications. We can use this to define a quadratic form,. In this chapter, you will learn about the quadratic forms of a matrix. Recall that a bilinear form from r2m → r can be written f(x, y) = xt ay where a is an m × m matrix. The.
Quadratic form Matrix form to Quadratic form Examples solved
See examples of geometric interpretation, change of. Recall that a bilinear form from r2m → r can be written f(x, y) = xt ay where a is an m × m matrix. We can use this to define a quadratic form,. Find a matrix \(q\) so that the change of coordinates \(\mathbf y = q^t\mathbf x\) transforms the quadratic form.
PPT Quadratic Forms, Characteristic Roots and Characteristic Vectors
Recall that a bilinear form from r2m → r can be written f(x, y) = xt ay where a is an m × m matrix. The quadratic forms of a matrix comes up often in statistical applications. Find a matrix \(q\) so that the change of coordinates \(\mathbf y = q^t\mathbf x\) transforms the quadratic form into one that has.
Quadratic Form (Matrix Approach for Conic Sections)
The matrix a is typically symmetric, meaning a t = a, and it determines. The quadratic form q(x) involves a matrix a and a vector x. See examples of geometric interpretation, change of. We can use this to define a quadratic form,. The quadratic forms of a matrix comes up often in statistical applications.
Solved (1 point) Write the matrix of the quadratic form Q(x,
The quadratic forms of a matrix comes up often in statistical applications. Learn how to define, compute and interpret quadratic forms as functions of symmetric matrices. The quadratic form q(x) involves a matrix a and a vector x. Find a matrix \(q\) so that the change of coordinates \(\mathbf y = q^t\mathbf x\) transforms the quadratic form into one that.
Definiteness of Hermitian Matrices Part 1/4 "Quadratic Forms" YouTube
Find a matrix \(q\) so that the change of coordinates \(\mathbf y = q^t\mathbf x\) transforms the quadratic form into one that has no. See examples of geometric interpretation, change of. In this chapter, you will learn about the quadratic forms of a matrix. The quadratic form q(x) involves a matrix a and a vector x. The matrix a is.
SOLVEDExpress the quadratic equation in the matr…
The quadratic form q(x) involves a matrix a and a vector x. The quadratic forms of a matrix comes up often in statistical applications. See examples of geometric interpretation, change of. Learn how to define, compute and interpret quadratic forms as functions of symmetric matrices. The matrix a is typically symmetric, meaning a t = a, and it determines.
The Matrix A Is Typically Symmetric, Meaning A T = A, And It Determines.
Find a matrix \(q\) so that the change of coordinates \(\mathbf y = q^t\mathbf x\) transforms the quadratic form into one that has no. Recall that a bilinear form from r2m → r can be written f(x, y) = xt ay where a is an m × m matrix. Learn how to define, compute and interpret quadratic forms as functions of symmetric matrices. The quadratic form q(x) involves a matrix a and a vector x.
The Quadratic Forms Of A Matrix Comes Up Often In Statistical Applications.
See examples of geometric interpretation, change of. We can use this to define a quadratic form,. In this chapter, you will learn about the quadratic forms of a matrix.