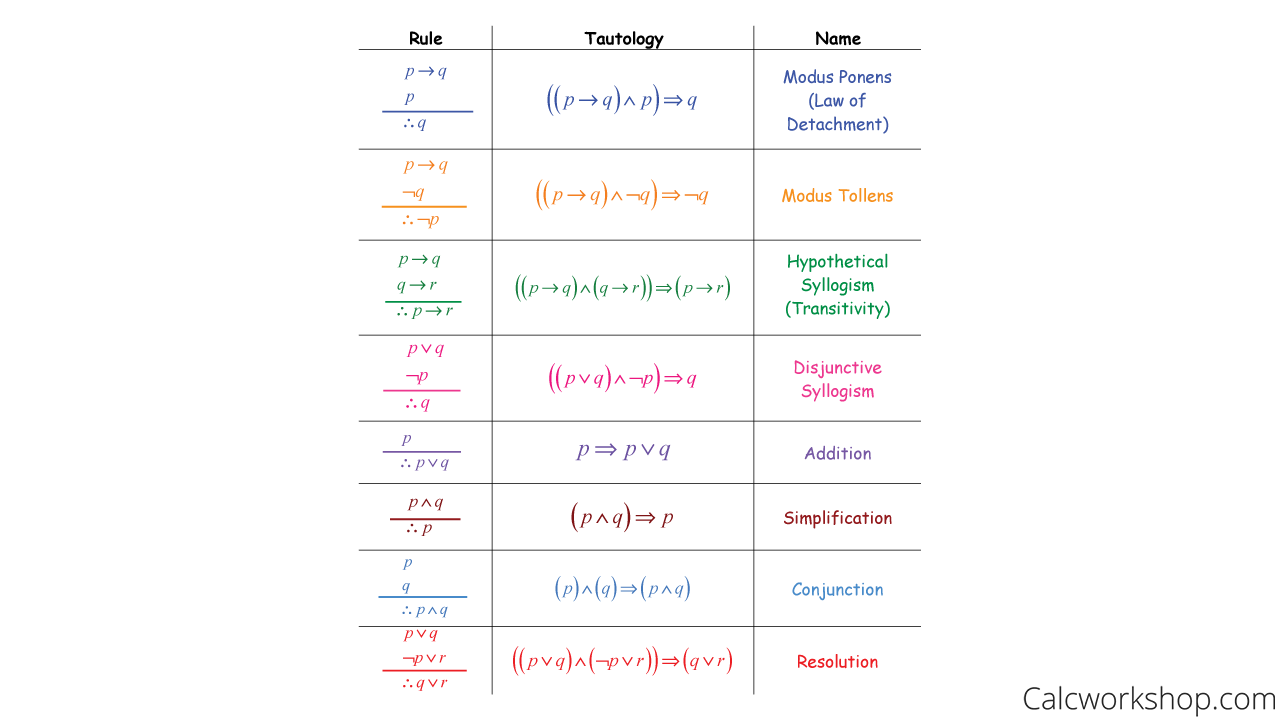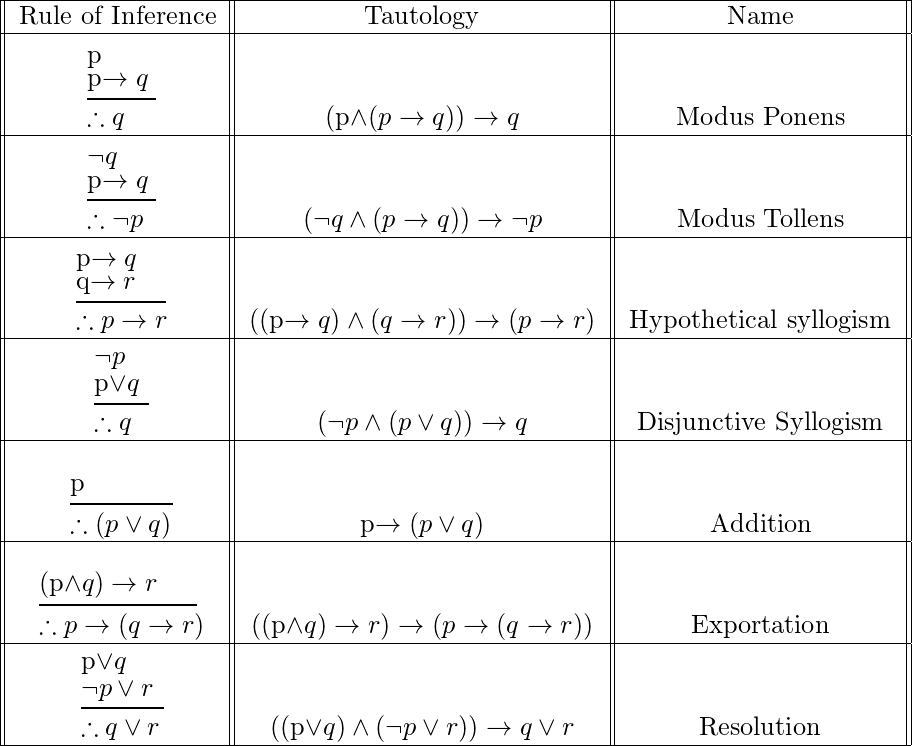Rules Of Inference Discrete Math
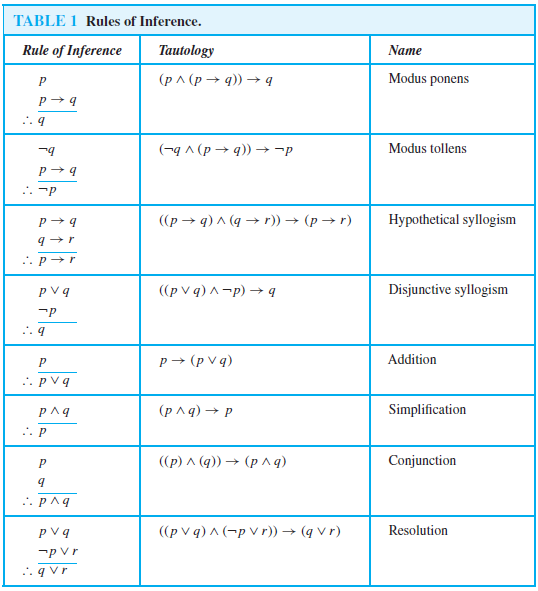
Rules Of Inference Discrete Math - A valid argument does not always mean you have a true conclusion; Rather, the conclusion of a valid argument must be true if all the premises are. Rules of inference are essential tools in logic and mathematics, enabling the derivation of conclusions from premises. Suppose there are two premises, p and p → q. Rules of inference for quantifiers example 1 given everyone in this discrete mathematics class has taken a course in computer science marla is a. There are various types of rules of inference, which are described as follows:
Rules of inference are essential tools in logic and mathematics, enabling the derivation of conclusions from premises. Suppose there are two premises, p and p → q. Rather, the conclusion of a valid argument must be true if all the premises are. Rules of inference for quantifiers example 1 given everyone in this discrete mathematics class has taken a course in computer science marla is a. There are various types of rules of inference, which are described as follows: A valid argument does not always mean you have a true conclusion;
Suppose there are two premises, p and p → q. A valid argument does not always mean you have a true conclusion; Rules of inference for quantifiers example 1 given everyone in this discrete mathematics class has taken a course in computer science marla is a. Rather, the conclusion of a valid argument must be true if all the premises are. There are various types of rules of inference, which are described as follows: Rules of inference are essential tools in logic and mathematics, enabling the derivation of conclusions from premises.
PPT Discrete Mathematics Rules of Inference and Proofs PowerPoint
Rules of inference are essential tools in logic and mathematics, enabling the derivation of conclusions from premises. Rules of inference for quantifiers example 1 given everyone in this discrete mathematics class has taken a course in computer science marla is a. Suppose there are two premises, p and p → q. A valid argument does not always mean you have.
Rules of Inference (Detailed w/ StepbyStep 7 Examples!)
Suppose there are two premises, p and p → q. Rules of inference for quantifiers example 1 given everyone in this discrete mathematics class has taken a course in computer science marla is a. There are various types of rules of inference, which are described as follows: Rather, the conclusion of a valid argument must be true if all the.
04 Rules of Inference and Proofs · Discrete Mathematics Explained in Detail
Rules of inference are essential tools in logic and mathematics, enabling the derivation of conclusions from premises. Suppose there are two premises, p and p → q. There are various types of rules of inference, which are described as follows: Rather, the conclusion of a valid argument must be true if all the premises are. Rules of inference for quantifiers.
Proofs Unofficial UCSC Student Guide
Rather, the conclusion of a valid argument must be true if all the premises are. There are various types of rules of inference, which are described as follows: Rules of inference are essential tools in logic and mathematics, enabling the derivation of conclusions from premises. A valid argument does not always mean you have a true conclusion; Suppose there are.
Rules_of_Inferences_Discrete_Mathematics_I_—_MATHCOSC_1056E_....pdf
Suppose there are two premises, p and p → q. A valid argument does not always mean you have a true conclusion; Rather, the conclusion of a valid argument must be true if all the premises are. Rules of inference are essential tools in logic and mathematics, enabling the derivation of conclusions from premises. There are various types of rules.
Inference Rules Discrete Mathematics Lecture Slides Docsity
Rather, the conclusion of a valid argument must be true if all the premises are. A valid argument does not always mean you have a true conclusion; Rules of inference are essential tools in logic and mathematics, enabling the derivation of conclusions from premises. There are various types of rules of inference, which are described as follows: Rules of inference.
RULES OF INFERENCE DISCRETE MATHEMATICS (Lesson Proper and Examples
Rules of inference are essential tools in logic and mathematics, enabling the derivation of conclusions from premises. Rules of inference for quantifiers example 1 given everyone in this discrete mathematics class has taken a course in computer science marla is a. There are various types of rules of inference, which are described as follows: Rather, the conclusion of a valid.
Discrete Math 1 Tutorial 29 Rules of Inference YouTube
A valid argument does not always mean you have a true conclusion; Rules of inference for quantifiers example 1 given everyone in this discrete mathematics class has taken a course in computer science marla is a. Rather, the conclusion of a valid argument must be true if all the premises are. Suppose there are two premises, p and p →.
Last Minute Notes Discrete Mathematics
Rules of inference are essential tools in logic and mathematics, enabling the derivation of conclusions from premises. Rather, the conclusion of a valid argument must be true if all the premises are. Rules of inference for quantifiers example 1 given everyone in this discrete mathematics class has taken a course in computer science marla is a. Suppose there are two.
PPT Discrete Mathematics PowerPoint Presentation ID264639
There are various types of rules of inference, which are described as follows: Rather, the conclusion of a valid argument must be true if all the premises are. Rules of inference are essential tools in logic and mathematics, enabling the derivation of conclusions from premises. Rules of inference for quantifiers example 1 given everyone in this discrete mathematics class has.
There Are Various Types Of Rules Of Inference, Which Are Described As Follows:
Suppose there are two premises, p and p → q. Rules of inference are essential tools in logic and mathematics, enabling the derivation of conclusions from premises. Rules of inference for quantifiers example 1 given everyone in this discrete mathematics class has taken a course in computer science marla is a. A valid argument does not always mean you have a true conclusion;